Loi bêta \({\mathcal B}(a,b)\)
Loià densité, donc la densité est donnée par : $$f_{a,b}:x\mapsto\frac{x^{a-1}(1-x)^{b-1} }{B(a,b)}\Bbb 1_{x\in[0,1]}$$avec \(B\) la
Fonction bêta.
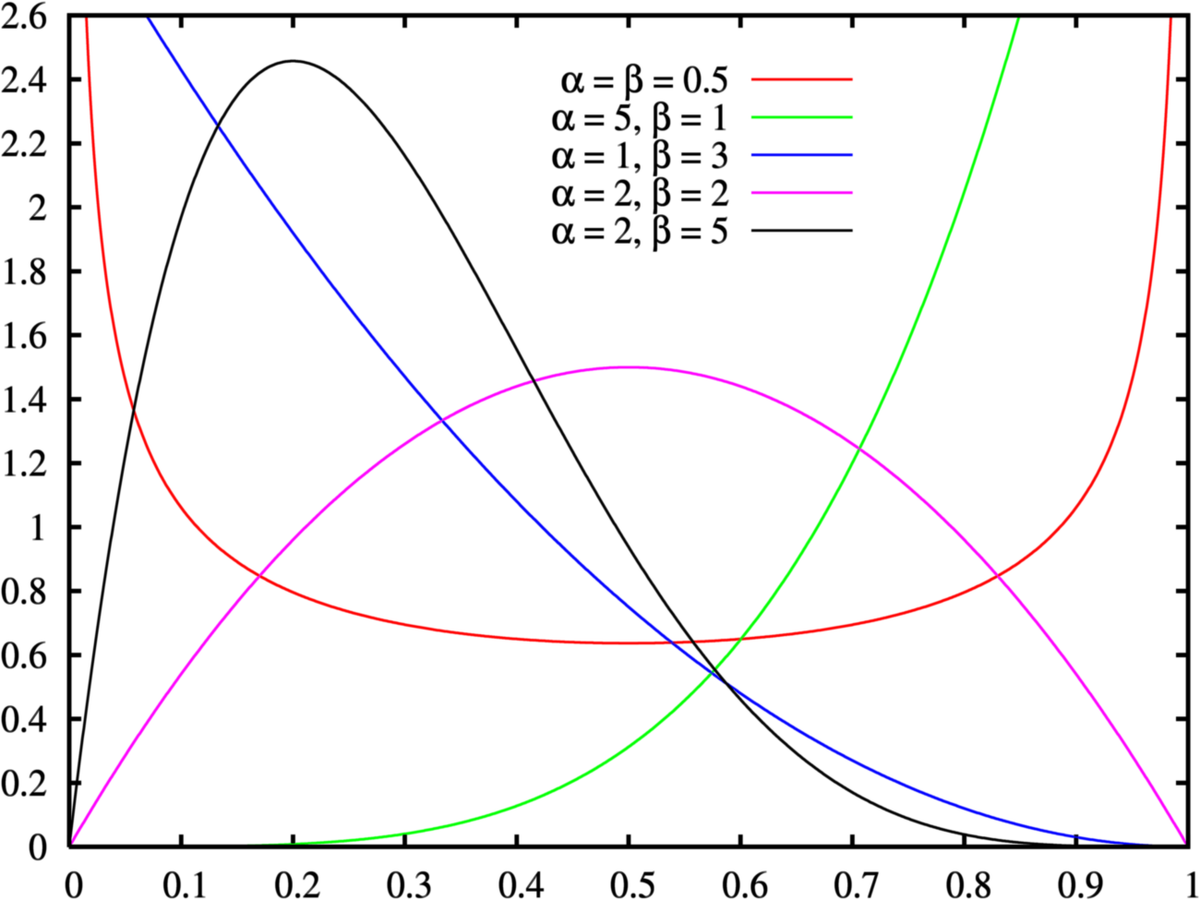
- espérance : \({\Bbb E}[X]=\) \(\frac{\alpha}{\alpha+\beta}\)
- variance : \(V(X)=\) \(\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\)
